A distance transform, or a distance map, is a map where each pixel represents the distance to the nearest boundary pixel. Take a look at the figure below.
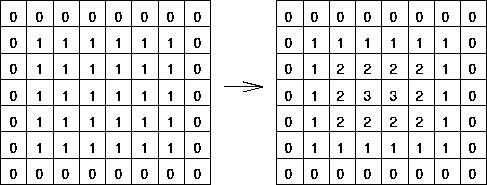
When using a distance transform, an appropriate metric for the distance should be chosen. For example, if you are an authentic engineer, you can measure a distance using the good old Euclidean distance; if you are a big fan of Piet Mondrian, then you can go with Manhattan distance; or if you are a professional chess player, you can try a Chessboard distance.
One more thing about the distance transform; a signed distance transform is a distance transform with signs. It has positive values at points inside the boundary, and negative values at points outside the boundary. On the boundary, the values are zero.
So… back to the detection map. The detection map can say something about the location of the curb. For example, if you are at pixel (250, 130), and the detection map has a value of 10, then you can tell that you are 10 units away from the nearest curb.
But be careful, the authors didn’t use vanilla distance transform. They used the inverse truncated distance transform. They used inverse distance transform because they wanted the values to be the maximum at the curb. Also, they used the truncated distance transform so that the points that are further away than the threshold distance have the value of zero.
Note that the detection map is a scalar field, i.e.,
\[S \in \mathbb{R}^{1 \times H \times W}\]
Leave a comment